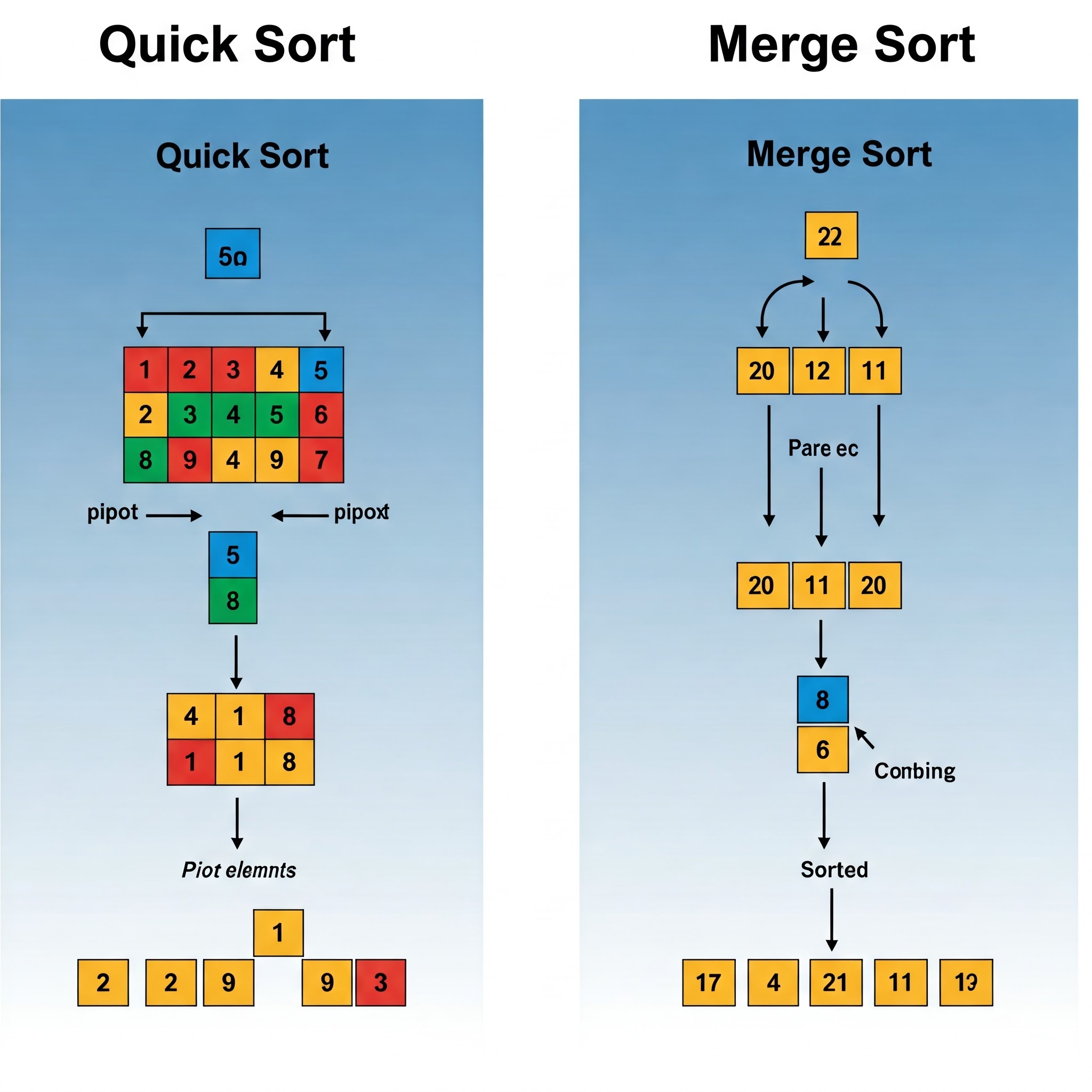
归并排序#
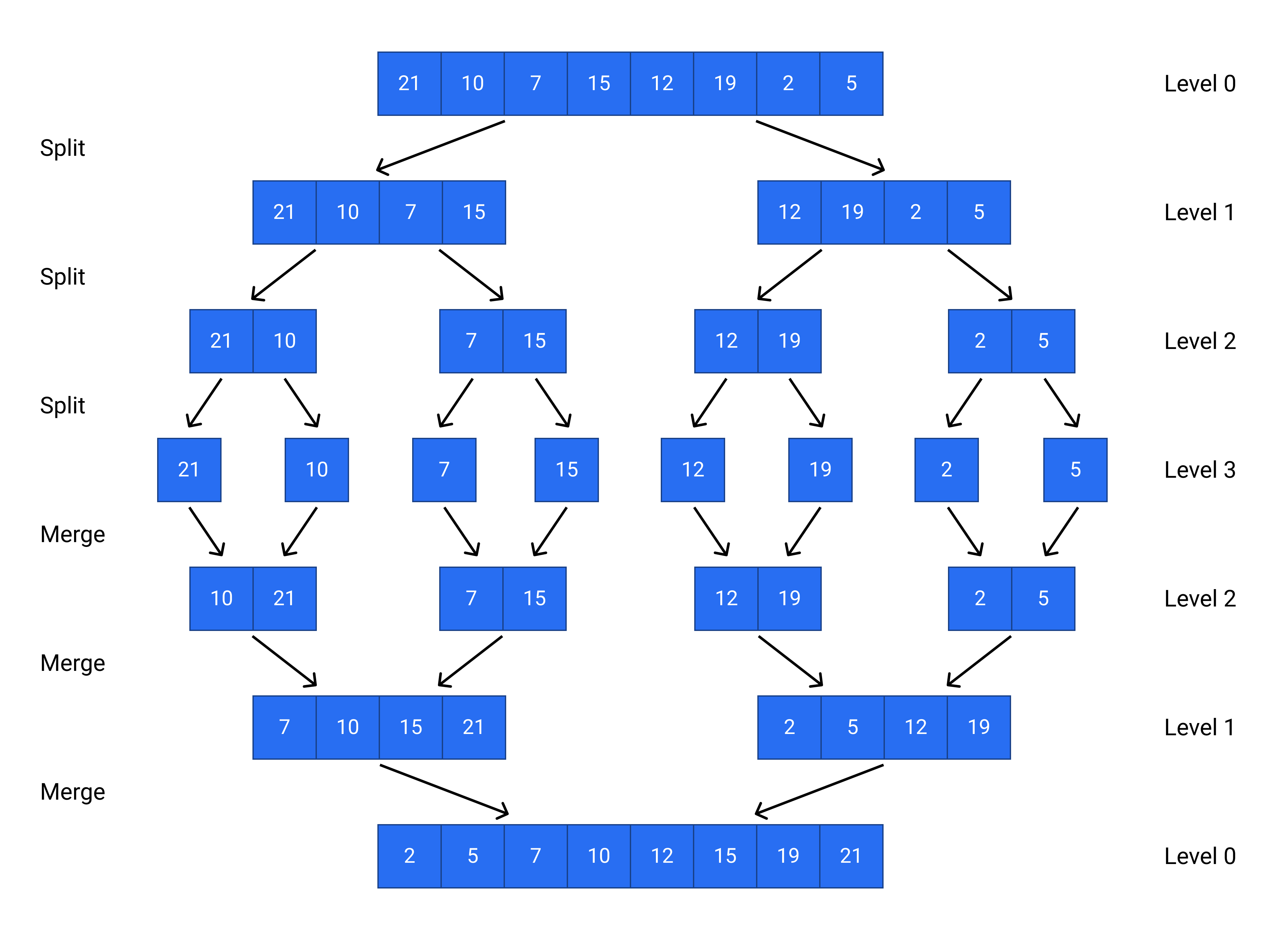
归并排序的步骤#
- 递归地把当前序列拆分为两个子序列,直到每个子序列只有一个元素
- 对每个子序列递归地调用归并排序
- 将两个有序子序列合并成一个最终的有序序列
- 重复步骤1~3,直到排序完成
归并排序的步骤实现#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| pub fn merge_sort(data: &mut [i32]) {
// base case
if data.len() <= 1 {
return;
}
let mid = data.len() / 2;
// recusive call two sub array
merge_sort(&mut data[0..mid]);
merge_sort(&mut data[mid..]);
// merge the two sorted sub array;
merge(data, 0, mid, data.len());
}
fn merge(data: &mut [i32], low: usize, mid: usize, high: usize) {
// copy left and right sub array
let left = &data[low..mid].to_vec();
let right = &data[mid..high].to_vec();
// keep two pointer to two sub array
let mut i = 0;
let mut j = 0;
// the merged array index
let mut k = low;
// the merge loop, increasing k from low to high;
while k >= low && k < high {
// assign the smaller value to data[k]
while i < left.len() && j < right.len() {
if left[i] <= right[j] {
data[k] = left[i];
i += 1;
} else {
data[k] = right[j];
j += 1;
}
k += 1;
}
// assign the rest value of left part to data[k..]
while i < left.len() {
data[k] = left[i];
i += 1;
k += 1;
}
// assign the rest value of right part to data[k..]
while j < right.len() {
data[k] = right[j];
j += 1;
k += 1;
}
}
}
|
快速排序#
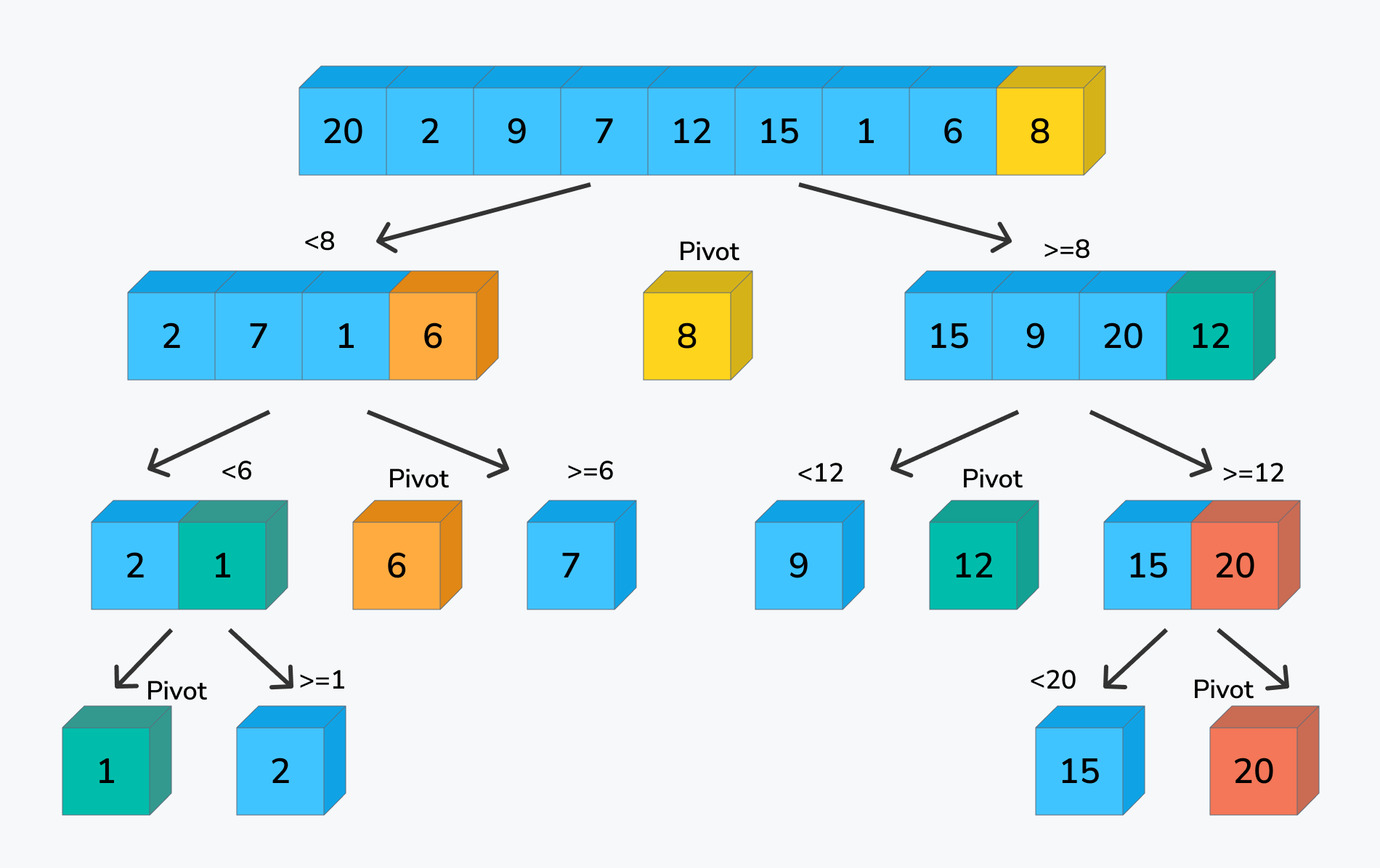
快速排序的步骤#
- 选取一个元素作为基准值
- 遍历整个数组,将比基准值小的元素放到基准值的左边,将比基准值大的元素放到基准值的右边
- 递归地对左右两边的子数组进行步骤1~2
- 重复步骤1~3,直到排序完成
原地快速排序的步骤实现#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| pub fn quick_sort(data: &mut [i32]) {
// base case; which also eliminate 0 - i overflow issue in partition fucntion.
if data.len() <= 1 {
return;
}
// always choose the last element(len() -1) as pivot element
let pos = partition(data, 0, data.len() - 1);
//if pos > 0 {
quick_sort(&mut data[0..pos]);
//}
quick_sort(&mut data[pos + 1..]);
}
fn partition(data: &mut [i32], low: usize, high: usize) -> usize {
let mut i = low;
// the last element is the pivot element
for j in low..high {
// swap the element which is smaller than pivot to the left part
if data[j] <= data[high] {
data.swap(i, j);
i += 1;
}
}
// swap the pivot element to the correct position
data.swap(i, high);
i
}
|
merge sort需要额外的空间,快排不需要额外的空间.
merge sort时刻需要注意,两个子数组都需要满足自己本身已经排好了,merge的过程中也不能破坏子数组本身的排序,
所以我们不能在merge中使用swap, swap大概率会打乱排序, 可以用shift, 但是不如使用额外的空间实现简单.
反之, 快排swap元素的时候很随意,不需要考虑左边是是否已经排序,只需要满足左边都比pivot小,右边都比pivot大就行.
| Feature | Merge Sort | Quicksort |
|---|
| Time Complexity | O(n log n) | O(n log n) avg, O(n^2) worst |
| Space Complexity | O(n) | O(log n) avg, O(n) worst |
| Stability | Stable | Unstable (default) |
| Implementation | More complex | Simpler (basic) |
| Practical Speed | Consistent | Generally faster |
| in palce | no | can be implement |